Mit diesem Rechner lassen sich Dezimalzahlen in einen BCD-Code und BCD-Codes in die Dezimalschreibweise umwandeln. BCD steht für "Binary Coded Decimal". Bei der Umwandlung von einem BCD-Code in eine Dezimalzahl werden keine Pseudotetraden akzeptiert.
Umwandlung dezimal zu BCD-Code
Um für eine Dezimalzahl den BCD-Code zu ermitteln muss jede Ziffer der Dezimalzahl nacheinander in eine Binärzahl bestehend aus 4 Bits umgewandelt werden. Wenn zum Beispiel in der Dezimalzahl eine 5 steht, wird diese 5 in "0101" umgewandelt. Die entstehenden 4-Bit-Blöcke werden "Nibble" genannt. Für die Umwandlung kann die folgende Tabelle genutzt werden:
| dezimal | binär |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
Beispiel Kodierung:
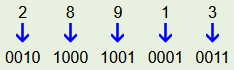
Als Beispiel soll die Zahl 28913 als BCD-Code dargestellt werden.
Der BCD-Code lautet also: 0010 1000 1001 0001 0011
Umwandlung BCD-Code nach dezimal
Um einen BCD-Code wieder zurück zu einer Dezimalzahl umzuwandeln wird die Zahl in 4-Bit-Blöcke aufgeteilt. Jeder 4-Bit-Block wird in das Dezimalsystem umgewandelt und die Dezimalziffern, die man erhält, werden aneinander gehangen.
Beispiel Dekodierung:
Der BCD-Code aus dem Beispiel oben soll wieder zurück in das Dezimalsystem umgewandelt werden.
Das Ergebnis lautet also 28913.
Pseudotetraden
Mit 4 Bits lassen sich 16 Ziffern darstellen. Zum Kodieren der Dezimalziffern werden aber nur 10 4-Bit-Kombinationen verwendet. Die übrigen 6 4-Bit-Kombinationen werden Pseudotetraden genannt und stehen für keine gültige Ziffer. Ihnen kann aber eine besondere Bedeutung zugewiesen werden (zum Beispiel Vorzeichen, Komma oder sonstige Zeichen).
Zahlen mit Komma
Es gibt verschiedene Strategien, um Zahlen mit Komma als BCD-Code abzuspeichern. Dafür lassen sich zum Beispiel Pseudotetraden nutzen. Eine andere Strategie kann sein, dass Zahlen immer mit der gleichen Anzahl an Vorkommastellen und der gleichen Anzahl an Nachkommastellen kodiert werden (Fixkommazahlen). In diesem Fall müssen gegebenenfalls vorne und hinten fehlende Nullen ergänzt werden.
Vorteile und Nachteile
Viele Kommazahlen lassen sich im IEEE-754-Gleitkommaformat nicht exakt darstellen, obwohl sie in der Dezimaldarstellung eigentlich sehr kompakt sind. Zum Beispiel lässt sich 7,1 nicht exakt darstellen. In einen BCD-Code lässt sich 7,1 hingegen ohne zu runden umwandeln. Berechnungen mit BCD-Codes sind aber umständlicher und somit langsamer als mit Gleitkommazahlen und durch die Pseudotetraden wird der Speicherbereich uneffizient genutzt.