Mit diesem Rechner lassen sich Binärzahlen in Hexadezimalzahlen und Hexadezimalzahlen in Binärzahlen umwandeln.
Wenn man eine Zahl von einem Zahlensystem mit der Basis a in ein Zahlensystem mit der Basis b umwandeln möchte, dann kann man die Zahl zuerst vom Zahlensystem mit der Basis a in das Dezimalsystem umwandeln und vom Dezimalsystem in das Zahlensystem mit der Basis b. Wenn man dies von Hand macht, dann kann das bei großen Zahlen sehr aufwändig werden. Für die Umwandlung vom Binärsystem in das Hexadezimalsystem bzw. umgekehrt gibt es aber einen Trick, mit dem man die Umwandlung sehr einfach und ohne elektronische Hilfsmittel durchführen kann. Dafür kann die folgende Tabelle hilfreich sein:
| Hexadezimal | Binär |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
| Hexadezimal | Binär |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| Hexadezimal | Binär |
|---|---|
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
binär in hexadezimal umrechnen
Wenn man eine Binärzahl in eine Hexadezimalzahl umrechnen möchte, unterteilt teilt man die Binärzahl in Blöcke auf. Mit Ausnahme vom vordersten Block müssen alle Blöcke aus genau 4 Bits bestehen. Der vorderste Block kann auch weniger als 4 Bits enthalten. Wenn man möchte, kann man diesen aber auch um führende 0-en auffüllen, sodass auch dieser aus 4 Bits besteht. Danach muss man nur noch jeden Block in das Hexadezimalsystem umwandeln. Bei 4-Bit-Blöcken lässt sich dies noch recht leicht im Kopf erledigen oder man kann auch eine Tabelle wie die von oben verwenden. Die Reihenfolge der Ziffern der Hexadezimalzahl entspricht der Reihenfolge der jeweiligen Blöcke der Binärzahl.
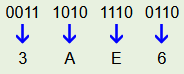
Als Beispiel soll 111010111001102 in das Hexadezimalsystem umgewandelt werden.
Im Hexadezimalsystem lautet die Zahl somit: 3AE616
binär in hexadezimal mit Komma:
Nach dem gleichen Prinzip kann man auch Kommazahlen vom Binärsystem in das Hexadezimalsystem umwandeln. Diesmal werden die Blöcke so aufgeteilt, dass alle Blöcke zwischen dem vordersten Block vom Vorkommateil und dem hintersten Block vom Nachkommateil genau 4 Bits enthalten. Die beiden Blöcke außen dürfen weniger als 4 Bits haben. Jeder Block darf nur Bits entweder vom Vorkommateil oder vom Nachkommateil enthalten. Wenn der hinterste Block vom Nachkommateil weniger als 4 Bits enthält, ist es wichtig, dass man dieses so behandelt, als wenn er hinten mit Nullen aufgefüllt aufgefüllt wäre. Wenn zum Beispiel der letzte Block vom Nachkommateil nur eine "1" enthält, wird dieser Block so behandelt, als wenn dort eine "1000" stehen würde. Um sich nicht zu vertun, kann es auch sinnvoll sein die zusätzlichen Nullen mit aufzuschreiben.
Als Beispiel soll die Zahl 1110101110,0110012 vom Binärsystem in das Hexadezimalsystem umgewandelt werden. Man rechnet:
Im Hexadezimalsystem lautet die Zahl somit: 3AE,6416
hexadezimal in binär umrechnen
Wenn man eine Zahl vom Hexadezimalsystem in das Binärsystem umwandeln möchte, muss man einfach nur jede Ziffer der Hexadezimalzahl in den entsprechenden 4-Bit-Block im Binärsystem umwandeln. Wenn der erste Block mit Nullen beginnt, dürfen diese entfernt werden.
Zum Beispiel soll 3A216 in das Binärsystem umgewandelt werden:
Die ersten beiden Nullen im vordersten Block können entfernt werden. Es gilt also: 3A216 ≙ 11101000102
hexadezimal in binär mit Komma:
Bei Kommazahlen verfährt man im Prinzip wie oben beschrieben. Wenn der letzte 4-Bit-Block mit Nullen endet, dürfen diese aber entfernt werden.
Als Beispiel soll 5,A4816 ins Binärsystem umgewandelt werden. Also rechnet man:
Die letzten 3 Nullen können entfernt werden. Es gilt also: 5,A4816 ≙ 101,1010010012