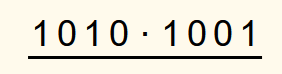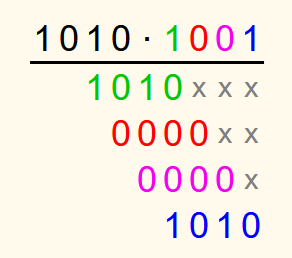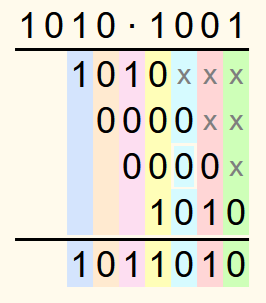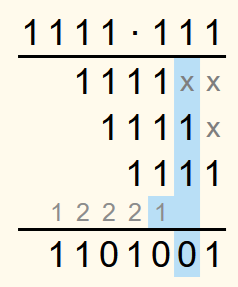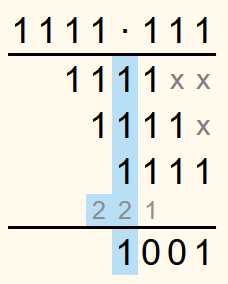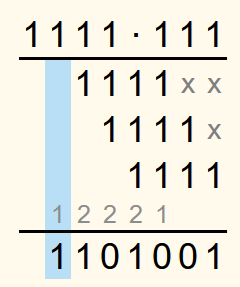Über den Rechner
Mit diesem Rechner lassen sich 2 Binärzahlen multiplizieren. Die Zahlen dürfen negativ sein und ein Komma enthalten.
Binärzahlen multiplizieren
2 Binärzahlen werden so ähnlich multipliziert wie 2 Dezimalzahlen. Zuerst werden die beiden zu multiplizierenden Binärzahlen aufgeschrieben.
Danach werden alle Ziffern von der zweiten Zahl mit der ersten Zahl multipliziert und so untereinander aufgeschrieben, dass die Zahl um so viele Stellen weiter nach links verschoben ist, wie Stellen hinter der aktuellen Ziffer in der zweiten Zahl sind. Zur besseren Übersichtlichkeit können die freien Stellen rechts von den Zahlen mit einem "x" oder einem Punkt versehen werden. Dies ist aber nicht nötig. Wenn es sich bei der aktuellen Ziffer um eine 0 handelt und das Produkt somit 0 ist, dann werden häufig anstatt nur einer 0 so viele Nullen aufgeschrieben, wie die erste Zahl Stellen hat.
Ob mit der vordersten oder der hintersten Ziffer der zweiten Zahl begonnen wird, ist egal.
Dann wird für jede Spalte, von rechts beginnend, die Summe der Zahlen in dieser Spalte berechnet. Wenn die Summe einer Spalte 0 oder 1 ist, wird sie in die Lösungszeile geschrieben.
Überträge:
Wenn die Summe der Zahlen einer Spalte größer als 1 ist, dann wird die letzte Ziffer der in eine Binärzahl umgewandelten Summe in die aktuelle Spalte der Lösungszeile geschrieben, und das, was vor der letzten Ziffer steht, wird in die Übertragszeile eine Spalte weiter links geschrieben. Die Überträge können als Binärzahlen aufgeschrieben werden. Dann muss aber beim Zusammenaddieren der nächsten Spalte berücksichtigt werden, dass es sich bei der Zahl in der Übertragszeile um eine Binärzahl handelt. Einfacher und kompakter ist es, wenn die Überträge als Dezimalzahlen aufgeschrieben werden.
Wenn zum Beispiel die Summe der Zahlen einer Spalte 3 ergibt, dann wird die Zahl zuerst in eine Binärzahl umgewandelt. Das ergibt 112. Die hintere 1 wird in die Lösungszeile geschrieben und die vordere 1 in die Übertragszeile.
Wenn die Summe der Zahlen einer Spalte 10 ergibt, dann ergibt das in eine Binärzahl umgewandelt 10102. Die hinterste 0 wird in die Lösungszeile geschrieben und 1012 wird in eine Dezimalzahl umgewandelt. Das ergibt 5. Und diese 5 wird in die Übertragszeile eine Spalte weiter links geschrieben.
Beispiel:
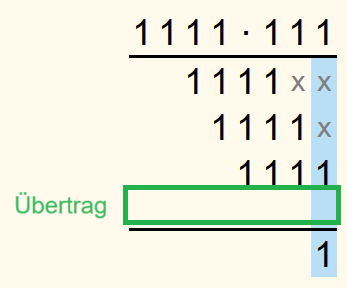
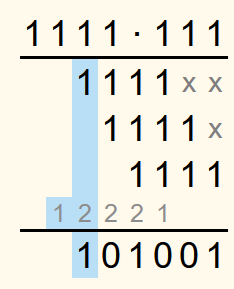
Als Beispiel soll 11112 ∙ 1112 berechnet werden.
In der letzten Spalte steht nur eine 1. Also wird die 1 in die Lösungszeile geschrieben.
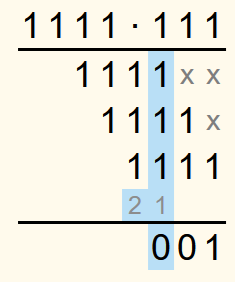
Die Summe der Zahlen der vorletzten Zeile ist 2. In eine Binärzahl umgewandelt ist dies 102. Die 0 wird in die Lösungszeile geschrieben und die 1 in die Übertragszeile eine Spalte weiter links.
In der nächsten Spalte ist die Summe der Zahlen 4. Das ist im Binärsystem 1002. Die 0 wird in die Lösungszeile geschrieben und weil 102 im Dezimalsystem 2 ist, wird in die Übertragszeile eine 2 geschrieben.
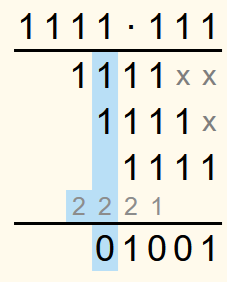
In der vierten Spalte von rechts ist die Summe 5. Das entspricht 1012. Also wird eine 1 in die Lösungszeile geschrieben und eine 2 in die Übertragszeile.
In der nächsten Spalte ist die Summe wieder 4 und somit wird eine 0 in die Lösungszeile eingetragen und der Übertrag ist 2.
Dann ist die Summe 3. Das entspricht 112. Also wird sowohl in die Lösungszeile als auch in die Übertragszeile jeweils eine 1 geschrieben.
alternative Berechnung der Überträge:
Die Summe einer Spalte muss zur Ermittlung der Zahl für den Übertrag und der Ziffer, die in die Lösungszeile geschrieben wird, nicht in eine Binärzahl umgewandelt werden. Stattdessen kann man die Summe auch durch 2 teilen. Wenn die Summe durch 2 teilbar ist, dann wird in die Lösungszeile eine 0 geschrieben, ansonsten eine 1. Für die Übertragszeile wird die Summe durch 2 geteilt und abgerundet.
Wenn zum Beispiel die Summe der Zahlen einer Spalte 5 ist, dann wird in die Lösungszeile eine 1 geschrieben, weil 5 nicht durch 2 teilbar ist. Zur Berechnung vom Übertrag wird 5 durch 2 geteilt. Das ergibt 2,5 und wenn man die 2,5 abrundet, dann erhält man 2.
Kommazahlen:
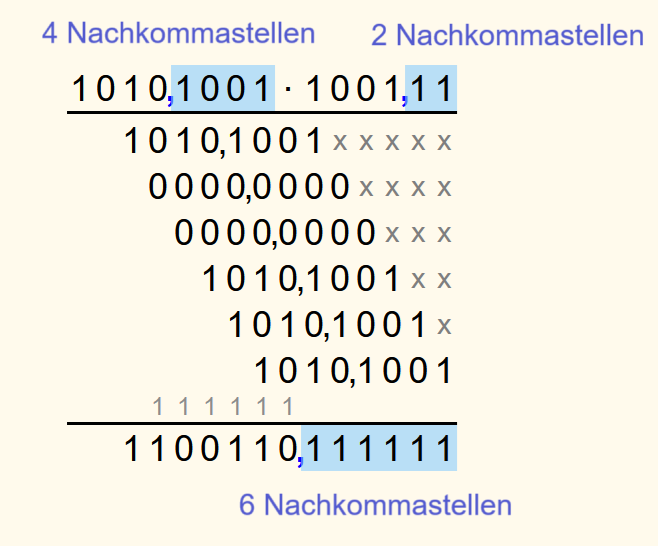
Wenn es sich bei mindestens einem der beiden Faktoren um eine Kommazahl handelt, dann wird so wie bei Binärzahlen ohne Komma jeder Ziffer der zweiten Zahl mit der ersten Zahl multipliziert. Die Kommas der ersten Zahl können dabei mit übernommen werden, sie können aber auch weggelassen werden.
Danach werden, wie bei der Multiplikation von Binärzahlen ohne Kommas, die Lösungszeile und die Übertragszeile berechnet. Dabei werden die Kommas nicht beachtet.
Das Komma wird in der Lösung so gesetzt, dass die Lösung so viele Nachkommastellen hat wie die beiden Faktoren zusammen.