Über den Rechner
Mit diesem Rechner lassen sich 2 binäre IEEE-754-Gleitkommazahlen addieren oder subtrahieren. Es kann ausgewählt werden, ob es sich bei den Eingabezahlen um binäre Gleitkommazahlen in binärer oder hexadezimaler Darstellung handelt oder ob es sich um Dezimalzahlen handelt. Wenn es sich um Dezimalzahlen handelt, dann werden sie vor dem Addieren oder Subtrahieren in binäre Gleitkommazahlen umgewandelt.
Aufbau
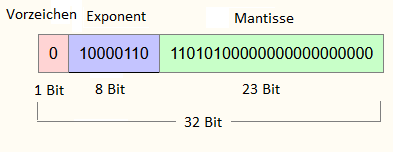
Eine binäre Gleitkommazahl setzt sich aus 3 Teilen zusammen. Sie beginnt mit einem Vorzeichenbit. Dieses ist 0, wenn die Zahl positiv ist oder 1, wenn sie negativ ist.
Darauf folgt ein Exponent (auch Charakteristik genannt). Dieser dient dazu, abzuspeichern, um wie viele Stellen das Komma der Binärzahl nach rechts oder links verschoben werden musste, um sie zu normalisieren. Der Exponent wird immer als positiver Wert abgespeichert. Damit auch ein Exponentwert abgespeichert werden kann, wenn das Komma zum Normalisieren nach rechts verschoben werden musste, wird zum Exponent ein Bias hinzuaddiert.
Auf den Exponent folgt eine Mantisse. Diese wird ermittelt, indem das Komma so weit nach links oder rechts verschoben wird, bis es genau hinter der ersten 1 der Binärzahl steht (Normalisierung). In die Mantisse werden dann die Nachkommastellen geschrieben.
| Datentyp | Größe | Exponent | Mantisse | Bias |
|---|---|---|---|---|
| binary16 | 16 Bits | 5 Bits | 10 Bits | 15 |
| binary32 | 32 Bits | 8 Bits | 23 Bits | 127 |
| binary64 | 64 Bits | 11 Bits | 52 Bits | 1023 |
| binary128 | 128 Bits | 15 Bits | 112 Bits | 16383 |
Addition binärer Gleitkommazahlen mit gleichem Vorzeichen
2 Zahlen, die sich im binären IEEE-754-Gleitkommaformat befinden und das gleiche Vorzeichen haben, können mit den folgenden Schritten addiert werden:
- Exponenten in Dezimalzahlen umwandeln
- Mantissen erweitern
- Komma verschieben, um Exponent anzugleichen
- Mantissen addieren
- Normalisieren
- Runden
- Exponent in Binärzahl umwandeln
- Gleitkommazahl zusammensetzen
Schritt 1 und Schritt 7 können ausgelassen werden, wenn man die Differenz der beiden Exponenten in binärer Form ermittelt und den Exponent bei Verschiebungen des Kommas in seiner binären Form anpasst.
Um das Vorgehen zu verdeutlichen, sollen die folgenden 2 binären Gleitkommazahlen addiert werden:
und
1. Exponenten in Dezimalzahlen umwandeln:
Als ersten Schritt wandelt man die beiden Exponenten der beiden binären Gleitkommazahlen in Dezimalzahlen um. Den Bias kann man abziehen, muss es aber nicht. In diesem Beispiel wird der Bias nicht vom Exponenten abgezogen.
2. Mantisse erweitern:
Als nächstes wird vor die beiden Mantissen "1," geschrieben:
In Kombination mit den Exponenten sind die Zahlen somit:
3. Komma verschieben, um Exponent anzugleichen:
Wenn sich die Exponenten der beiden Zahlen unterscheiden, dann berechnet man die Differenz des größeren und des kleineren Exponenten. Dann wird das Komma der Zahl mit dem kleineren Exponenten um so viele Stellen nach links verschoben, wie die Differenz groß ist. Der Exponent wird dementsprechend angepasst und ist hinterher bei beiden Zahlen gleich groß.
Die Differenz der beiden Exponenten ist 4 und der Exponent der zweiten Zahl ist kleiner als der von der ersten Zahl. Deshalb muss das Komma der zweiten Zahl um 4 Stellen nach links verschoben werden.
4. Mantissen addieren:
Die Mantissen werden im Prinzip so addiert, wie man es bei der Addition von 2 Dezimalzahlen gewohnt ist. Die beiden Zahlen werden so untereinander geschrieben, dass die Kommas der beiden Zahlen untereinander stehen. Entweder unter den beiden Zahlen oder darüber wird eine Zeile für den Übertrag freigehalten. Dann werden von rechts beginnend immer das Zeichen der oberen Zahl, das Zeichen der unteren Zahl und falls vorhanden der Übertrag zusammenaddiert. Wichtig ist, dass die Summe der Zeichen immer eine Binärzahl ist. Also 102 statt 2 und 112 statt 3. Wenn die Summe der Zeichen einer Spalte aus einem Zeichen besteht, wird dieses in der gleichen Spalte unter den Lösungsstrich geschrieben, und wenn sie aus 2 Zeichen besteht, dann wird das hintere Zeichen unter den Lösungsstrich geschrieben und das vordere Zeichen wird in die Zeile für den Übertrag eine Spalte weiter links geschrieben.
| 1 | , | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| + | 0 | , | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 0 | , | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
5. Normalisieren:
Es kann vorkommen, dass nach dem Addieren das Komma nicht mehr hinter der ersten 1 steht. In diesem Fall muss das Komma wieder hinter die erste 1 verschoben werden und der Exponent wird entsprechend angepasst.
Das Komma muss um eine Stelle nach links verschoben werden, damit es hinter der ersten 1 steht.
1,00000011011110101000110111012 ∙ 2135 − Bias
6. Runden:
Die Zahl muss so gerundet werden, dass hinterher nur noch maximal so viele Stellen hinter dem Komma stehen, wie in der Mantisse der binären Gleitkommazahl gespeichert werden können. Bei Gleitkommazahlen mit 32 Bits wären dies zum Beispiel 23.
Es gibt verschiedene Rundungsmodi. Es kann immer aufgerundet, immer abgerundet oder immer Richtung 0 gerundet werden. Am sinnvollsten und am häufigsten verwendet ist aber die Rundung zur nächsten darstellbaren Zahl. Dafür wird sich angesehen, was auf das niederwertigste Bit (das letzte Bit, welches in die Mantisse passt) folgt. Wenn auf das niederwertigste Bit eine 0 folgt, dann ist die Zahl näher an der betragsmäßig kleineren darstellbaren Zahl. Wenn auf das niederwertigste Bit eine 1 folgt und danach an irgendeiner Stelle noch eine weitere 1 steht, dann ist die Zahl näher an der betragsmäßig größeren Zahl. Wenn das Bit hinter dem niederwertigsten Bit eine 1 ist und danach nicht an irgendeiner Stelle noch eine 1 steht, dann ist die Zahl genau zwischen 2 darstellbaren Zahlen, und dann wird so gerundet, dass hinterher eine 0 im niederwertigsten Bit steht.
Bei Gleitkommazahlen mit 32 Bits stehen 23 Bits für die Mantisse zur Verfügung. Die Zahl hat aber 28 Nachkommastellen. Deshalb muss sie gerundet werden.
1,00000011011110101000110111012 ∙ 2135 − Bias
Das letzte Bit, welches in die Mantisse passt, ist rot markiert. Da das Bit hinter diesem Bit eine 1 ist und danach noch mehrere Einsen folgen, ist die Zahl näher an der nächstgrößeren darstellbaren Zahl und deshalb muss aufgerundet werden.
1,000000110111101010001112 ∙ 2135 − Bias
7. Exponent in Binärzahl umwandeln
Wenn im ersten Schritt der Bias abgezogen wurde, dann muss er nun wieder zum Exponenten hinzuaddiert werden. Dann wird der "biased" Exponent in eine Binärzahl umgewandelt.
135 in eine Binärzahl umgewandelt ist: 100001112
8. Gleitkommazahl zusammensetzen:
Zum Schluss werden alle Komponenten zu einer binären Gleitkommazahl im IEEE-754-Standard zusammengesetzt.
Das Vorzeichenbit entspricht dem Vorzeichenbit der beiden Summanden.
In den Exponententeil werden die in Schritt 7 berechneten Exponentenbits geschrieben. Falls die Exponentenbits nicht ausreichen, um den Exponententeil vollständig auszufüllen, wird der Exponententeil vorne mit Nullen aufgefüllt.
In den Mantissenteil werden die Bits geschrieben, die hinter dem Komma stehen. Falls diese Bits nicht ausreichen, um die Mantisse vollständig auszufüllen, wird die Mantisse mit Nullen am hinteren Ende aufgefüllt.
Subtraktion binärer Gleitkommazahlen mit gleichem Vorzeichen
2 Zahlen, die sich im binären IEEE-754-Gleitkommaformat befinden und das gleiche Vorzeichen haben, können mit den folgenden Schritten subtrahiert werden:
- Exponenten in Dezimalzahlen umwandeln
- Mantissen erweitern
- Komma verschieben, um Exponent anzugleichen
- Mantissen subtrahieren
- Normalisieren
- Runden
- Exponent in Binärzahl umwandeln
- Gleitkommazahl zusammensetzen
Die Subtraktion von 2 binären Gleitkommazahlen unterscheidet sich von der Addition binärer Gleitkommazahlen hauptsächlich in Schritt 4.
Um das Vorgehen zu verdeutlichen, sollen die folgenden 2 binären Gleitkommazahlen subtrahiert werden:
1. Exponenten in Dezimalzahlen umwandeln:
Als Erstes werden die Exponenten in Dezimalzahlen umgewandelt. Den Bias kann man abziehen, man muss es aber nicht.
| 011110002 | ≙ | 26 + 25 + 24 + 23 |
| = | 64 + 32 + 16 + 8 | |
| = | 120 |
| 011110112 | ≙ | 26 + 25 + 24 + 23 + 21 + 20 |
| = | 64 + 32 + 16 + 8 + 2 + 1 | |
| = | 123 |
2. Mantissen erweitern:
Die beiden Mantissen werden um "1," erweitert.
3. Komma verschieben, um Exponent anzugleichen:
Wenn sich die beiden Exponenten unterscheiden, wird die Differenz vom größeren Exponentwert und dem kleineren Exponentwert berechnet. Danach wird das Komma der Zahl mit dem kleineren Exponenten um so viele Stellen nach links verschoben, wie die Differenz groß ist. Danach ist der Exponent beider Zahlen gleich.
Der Exponent von Zahl 1 ist kleiner als der von Zahl 2 und die Differenz der Exponenten ist 3. Deshalb muss das Komma von Zahl 1 um 3 Stellen nach links verschoben werden und der Exponent entsprechend angepasst werden.
0,0011101011011100000012 ∙ 2123 − Bias
4. Mantissen subtrahieren:
Wenn man im Dezimalsystem subtrahieren möchte und der Subtrahend größer als der Minuend ist, dann vertauscht man den Minuend und den Subtrahend und wechselt beim Ergebnis das Vorzeichen. Wenn man zum Beispiel 3 − 5 berechnen möchte, dann berechnet man zuerst 5 − 3 und schreibt vor das Ergebnis ein Minuszeichen. So macht man es auch bei Binärzahlen.
Um 2 Zahlen zu subtrahieren können das Ergänzungsverfahren oder das Abziehverfahren verwendet werden.
Ergänzungsverfahren:
Die Zahlen werden so untereinander geschrieben, dass deren Kommas untereinander stehen. Die größere der beiden Zahlen muss immer oben stehen. Unter den beiden Zahlen wird noch eine Zeile frei gelassen.
Die zweite Zahl ist größer als Erste und deshalb muss die zweite Zahl oben stehen.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , |
Dann werden die Spalten von rechts nach links durchgegangen und es wird von der oberen Ziffer die Untere abgezogen.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Wenn die untere Ziffer größer als die obere Ziffer ist, dann muss die obere Ziffer um eine führende 1 ergänzt werden. Diese Ziffer wird eine Spalte weiter links unter die untere Zahl geschrieben. Wichtig ist, dass die um die 1 ergänzte obere Ziffer als Binärzahl gelesen wird. Also 102 = 2 oder 112 = 3.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | ||||||||||||||||||||||||
| , | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Wenn in einer Spalte unter der unteren Zahl eine 1 steht, dann wird diese in Gedanken zur unteren Ziffer hinzuaddiert, bevor sie von der oberen Ziffer abgezogen wird. Wenn die Summe größer ist als die obere Ziffer, dann muss die obere Ziffer wieder ergänzt werden.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | |||||||||||||||||||||||
| , | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||
| 0 | , | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Da der Minuend und der Subtrahend vertauscht wurden, muss vom Ergebnis das Vorzeichen geändert werden.
Abziehverfahren:
Auch beim Abziehverfahren werden die Zahlen so untereinander geschrieben, dass deren Kommas untereinander stehen. Die größere der beiden Zahlen muss immer oben stehen.
Die zweite Zahl ist größer als Erste und deshalb muss die zweite Zahl oben stehen.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , |
Die Spalten werden von rechts nach links durchgegangen und wenn die untere Ziffer nicht größer ist als die Obere, dann wird die untere Ziffer wie beim Ergänzungsverfahren von der oberen abgezogen.
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Wenn die untere Ziffer größer ist als die Obere, dann muss die obere Ziffer durch eine führende 1 ergänzt werden. Diese 1 wird von der oberen Ziffer eine Spalte weiter links abgezogen. Dies kann man aufschreiben, indem man die Ziffer, die ergänzt wird oder von der 1 abgezogen wird, durchstreicht und die Zahl, durch die sie ersetzt wird darüber schreibt. Wichtig ist, dass die Zahlen nicht als Dezimalzahlen, sondern als Binärzahlen interpretiert werden. 10 steht also für die dezimale 2.
| 0 | 10 | |||||||||||||||||||||||
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Die untere Ziffer ist größer als die geänderte obere Ziffer. Also wird die geänderte obere Ziffer um eine führende 1 ergänzt und die obere Ziffer eine Spalte weiter links wird um 1 verringert.
| 0 | 10 | 10 | ||||||||||||||||||||||
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Wenn die obere Ziffer der aktuellen Spalte um eine 1 ergänzt werden soll und in der Spalte eine Stelle weiter links die obere Ziffer 0 ist, dann muss die obere Ziffer in der linken Spalte auch zuerst um eine 1 ergänzt werden, bevor sie um 1 reduziert werden kann, und die obere Ziffer noch eine Spalte weiter links muss um 1 reduziert werden. Und wenn es sich bei dieser auch um eine 0 handelt, dann muss sie auch ergänzt werden usw..
| 0 | 10 | 10 | 10 | 0 | 10 | 10 | ||||||||||||||||||
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| , | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 10 | 10 | 10 | 10 | 10 | 0 | 10 | 10 | 10 | 10 | 0 | 10 | 10 | |||||||||||
| 1 | , | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| − | 0 | , | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | , | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Da der Minuend und der Subtrahend vertauscht wurden, muss vom Ergebnis das Vorzeichen geändert werden.
5. Normalisieren:
Wenn das Komma nicht hinter der ersten 1 steht, dann muss das Komma dorthin verschoben werden. Der Exponent wird entsprechend angepasst.
Das Komma steht nicht hinter der ersten 1. Deshalb muss das Komma verschoben werden.
-1,1011011010110110000012 ∙ 2122 − Bias
6. Runden:
Wenn die Zahl mehr Nachkommastellen als die Mantisse der binären Gleitkommazahl Bits hat, dann muss die Zahl gerundet werden. Der am häufigsten verwendete und für die meisten Anwendungsgebiete sinnvollste Rundungsmodus ist die Rundung zur nächstgelegenen darstellbaren Zahl. Wenn die Zahl genau zwischen 2 darstellbaren Zahlen liegt (das Zeichen hinter dem niederwertigsten Bit ist eine 1 und darauf folgt nicht noch eine 1 an irgendeiner Stelle), dann wird zu der Zahl gerundet, die eine 0 im niederwertigsten Bit hat.
Die Zahl hat 21 Nachkommastellen. Diese passen in die 23 Bits der Mantisse. Somit muss die Zahl nicht gerundet werden.
7. Exponent in Binärzahl umwandeln:
Wenn in Schritt 1 der Bias herausgerechnet wurde, dann wird er nun wieder hinzuaddiert. Dann wird der den Bias enthaltende Exponent in eine Binärzahl umgewandelt.
122 ist in eine Binärzahl umgewandelt: 11110102
8. Gleitkommazahl zusammensetzen:
Am Schluss werden alle 3 Teile der binären Gleitkommazahl zusammengesetzt.
Wenn die erste Zahl größer als die zweite Zahl ist, dann entspricht das Vorzeichen dem Vorzeichen der beiden Eingabezahlen. Ansonsten muss es gewechselt werden.
In den Exponententeil wird die in Schritt 7 berechnete Binärzahl geschrieben. Wenn diese nicht alle Exponentenbits belegt, dann wird der Exponententeil vorne mit Nullen aufgefüllt.
In die Mantisse werden die Nachkommastellen der normalisierten und gerundeten Binärzahl geschrieben. Wenn diese die Mantisse nicht komplett ausfüllen, dann wird diese hinten mit Nullen aufgefüllt.
Das Ergebnis ist:
Die Zahl ist negativ, weil die erste Zahl kleiner als die Zweite ist und die beiden Zahlen deshalb zum Subtrahieren vertauscht werden mussten.
binäre Gleitkommazahlen mit unterschiedlichen Vorzeichen
Um 2 binäre IEEE-754-Gleitkommazahlen wie oben beschrieben zu addieren oder zu subtrahieren, müssen diese das gleiche Vorzeichen besitzen. Wenn dies nicht der Fall ist, dann lässt sich die Berechnung trotzdem durchführen, indem zuerst von einer der beiden Zahlen das Vorzeichen umgeändert wird, und danach wird statt einer Addition eine Subtraktion durchgeführt oder statt einer Subtraktion eine Addition.