Über den Rechner
Mit diesem Rechner lassen sich 2 binäre IEEE-754-Gleitkommazahlen dividieren. Es kann ausgewählt werden, ob es sich bei den Eingabezahlen um binäre Gleitkommazahlen in binärer oder hexadezimaler Darstellung handelt oder ob es sich um Dezimalzahlen handelt. Wenn es sich um Dezimalzahlen handelt, dann werden sie vor dem Dividieren in binäre Gleitkommazahlen umgewandelt.
Wichtige Werte:
| Datentyp | Größe | Exponent | Mantisse | Bias |
|---|---|---|---|---|
| binary16 | 16 Bits | 5 Bits | 10 Bits | 15 |
| binary32 | 32 Bits | 8 Bits | 23 Bits | 127 |
| binary64 | 64 Bits | 11 Bits | 52 Bits | 1023 |
| binary128 | 128 Bits | 15 Bits | 112 Bits | 16383 |
Binäre Gleitkommazahlen dividieren
2 Zahlen, die sich im binären IEEE-754-Gleitkommaformat befinden, können mit den folgenden Schritten dividiert werden:
- Exponenten in Dezimalzahlen umwandeln
- Mantissen erweitern
- Vorzeichen ermitteln
- Exponenten subtrahieren und Bias hinzuaddieren
- Mantissen dividieren
- Normalisieren
- Runden
- Exponent in Binärzahl umwandeln
- Gleitkommazahl zusammensetzen
Um das Vorgehen zu verdeutlichen, soll
durch
geteilt werden.
1. Exponenten in Dezimalzahlen umwandeln:
Zuerst werden die Exponenten der beiden binären Gleitkommazahlen in Dezimalzahlen umgewandelt. Der Bias kann herausgerechnet werden, aber dies ist nicht nötig und wird im Beispiel nicht gemacht.
2. Mantissen erweitern
Danach wird vor die beiden Mantissen ein "1," geschrieben.
In Kombination mit den Exponenten und den Vorzeichenbits sind die Zahlen somit:
3. Vorzeichen ermitteln
Wenn beide Gleitkommazahlen das gleiche Vorzeichen haben, dann ist der Quotient positiv und das Vorzeichenbit 0. Wenn sich die Vorzeichenbits der beiden Gleitkommazahlen unterscheiden, dann ist der Quotient negativ und das Vorzeichenbit 1.
Die Vorzeichenbits sind gleich. Somit ist das Vorzeichenbit der Lösung 0.
4. Exponenten subtrahieren und Bias hinzuaddieren
Vom Exponent des Dividenden wird der Exponent des Divisors abgezogen. Wenn der Bias in Schritt 1 nicht von den beiden Exponenten abgezogen worden ist, dann muss zur Differenz der Bias hinzuaddiert werden.
| 134 − 130 + Bias | = | 134 − 130 + 127 |
| = | 4 + 127 | |
| = | 131 |
5. Mantissen dividieren
Als Nächstes wird die Mantisse vom Dividenden durch die Mantisse vom Divisor geteilt. Das Dividieren von Binärzahlen funktioniert im Prinzip wie das Dividieren von Dezimalzahlen.
Die Kommas des Dividenden und des Divisors werden um gleich viele Stellen so weit nach rechts verschoben, bis der Divisor keine Nachkommastellen mehr hat.
Danach wird der Dividend von links beginnend Ziffer für Ziffer durchgegangen. In jedem Schritt wird die aktuelle Ziffer heruntergebracht. Das heißt, dass im ersten Schritt die erste Ziffer unter die erste Ziffer geschrieben wird und danach wird in jedem Schritt die aktuelle Ziffer neben die Zahl geschrieben, die aktuell die unterste Zahl in der Berechnung ist. Wenn danach die unterste Zahl kleiner als der Divisor ist, dann wird eine 0 an die Lösung angehängt. Das Anhängen einer 0 an die Lösung kann ausgelassen werden, wenn die Lösung bisher leer ist und wenn die aktuelle Ziffer nicht direkt vor einem Komma steht oder die letzte Ziffer des Dividenden ist. Wenn die aktuell unterste Zahl der Berechnung nicht kleiner als der Divisor ist, dann wird eine 1 an die Lösung angehängt und von der aktuell untersten Zahl der Berechnung wird der Divisor abgezogen. Wenn beim Dividenden ein Komma erreicht ist oder wenn gerade alle Ziffern vom Dividenden einmal heruntergebracht worden sind und die Lösung noch kein Komma enthält, dann wird an die Lösung ein Komma angehängt. Wenn alle Ziffern vom Dividenden "aufgebraucht" sind, die unterste Zahl der Berechnung noch nicht 0 ist und noch weiter gerechnet werden soll, dann werden in den folgenden Schritten jeweils eine 0 an die unterste Zahl angehängt. Es wird so lange gerechnet, bis alle Ziffern vom Dividenden einmal heruntergebracht worden sind und bis entweder die unterste Zahl 0 ist oder bis hinter der ersten 1 der Lösung so viele Ziffern stehen wie in die Mantisse passen plus eine zusätzliche Ziffer für das Runden.
Die Mantisse vom Divisor hat nach dem Voranstellen vom "1," und nach dem Streichen der hinteren Nullen 5 Nachkommastellen. Also muss von beiden Mantissen das Komma um 5 Stellen nach rechts verschoben werden.

Nach dem Herunterbringen der ersten 5 Ziffern des Dividenden ist die unterste Zahl der Berechnung kleiner als der Divisor. Da das Komma noch nicht erreicht wurde und die Lösung bisher leer ist, müssen die Nullen aber nicht an die Lösung angehängt werden.
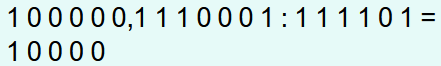
Auch nach dem Herunterbringen der sechsten Ziffer ist die Zahl noch kleiner als der Divisor. Da auf die sechste Ziffer ein Komma folgt, muss diesmal eine 0 in die Lösung geschrieben werden. Und danach wird ein Komma an die Lösung angehängt.

Nachdem die 1 heruntergebracht wurde, ist die unterste Zahl diesmal größer als der Divisor und deshalb wird eine 1 an die Lösung angehängt und der Divisor wird von der untersten Zahl abgezogen.
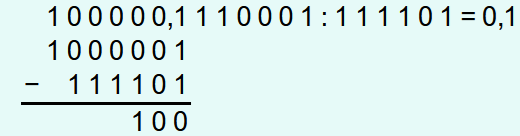
Nach dem Herunterbringen der nächsten 1 ist die unterste Zahl kleiner als der Divisor und deshalb wird eine 0 an die Lösung angehängt.
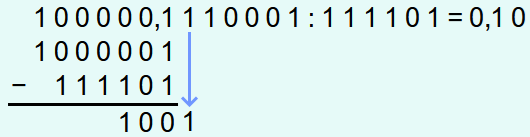
Auch bei den nächsten beiden Schritten ist die unterste Zahl kleiner als der Divisor und somit werden 2 Nullen an die Lösung angehängt.
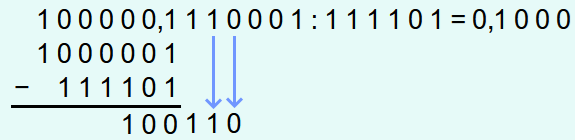
Nach dem Herunterbringen der nächsten 0 ist die unterste Zahl größer als der Divisor und deshalb wird eine 1 an die Lösung angehängt und der Divisor wird von der untersten Zahl abgezogen.
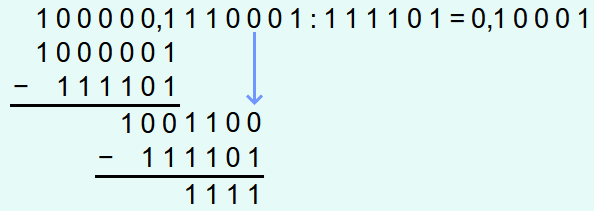
Im nächsten Schritt ist die unterste Zahl wieder kleiner als der Divisor.
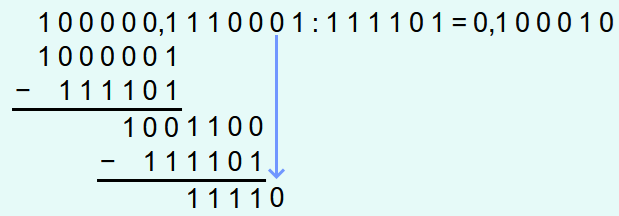
Und danach ist die unterste Zahl gleich dem Divisor und deshalb wird eine 1 angehängt und der Divisor abgezogen.

Da alle Ziffern des Dividenden aufgebraucht sind und ganz unten eine 0 steht, ist nun die exakte Lösung gefunden worden.
6. Normalisieren
Wenn das Komma vom Quotienten nicht hinter der ersten 1 steht, dann muss es verschoben werden. Wenn das Komma verschoben werden muss, dann wird auch der Exponent entsprechend angepasst. Wenn das Komma um eine Stelle nach rechts verschoben werden muss, dann wird der Exponent um 1 reduziert.
Das Komma muss um eine Stelle nach rechts verschoben werden. Deshalb muss der Exponent um 1 verringert werden.
1,0001012 ∙ 2130 − Bias
7. Runden
Wenn der Quotient mehr Nachkommastellen hat, als Ziffern in die Mantisse der binären Gleitkommazahl passen, muss der Quotient gerundet werden. Normalerweise wird zur nächsten darstellbaren Zahl gerundet. Dafür wird sich die Ziffer hinter dem niederwertigsten Bit angesehen. Das niederwertigste Bit ist das letzte Bit, für welches in der Mantisse noch Platz ist. Wenn die Ziffer hinter dem niederwertigsten Bit eine 1 ist und danach keine weitere 1 folgt (und die Berechnung auch nicht abgebrochen wurde), dann liegt der Quotient genau in der Mitte zwischen 2 darstellbaren Zahlen. In diesem Fall wird so gerundet, dass das niederwertigste Bit nach dem Runden 0 ist. Wenn die Ziffer hinter dem niederwertigsten Bit 0 ist, dann ist die nächstgelegene darstellbare Zahl die betragsmäßig kleinere Zahl. Wenn die Ziffer hinter dem niederwertigsten Bit eine 1 ist und wenn danach an mindestens einer weiteren Stelle eine 1 steht (bzw. die Berechnung abgebrochen worden ist), dann ist die betragsmäßig größere darstellbare Zahl die nächstgelegene darstellbare Zahl.
Beim Beispiel hat die Zahl 6 Nachkommastellen. Die Mantisse einer binären Gleitkommazahl mit 32 Bits hat Platz für 23 Bits. Deshalb muss die Zahl nicht gerundet werden.
8. Exponent in Binärzahl umwandeln
Der Exponent wird danach in eine Binärzahl umgewandelt. Wenn in Schritt 1 der Bias abgezogen worden ist, dann muss er in diesem Schritt vor der Umwandlung in eine Binärzahl wieder hinzuaddiert werden.
130 ist in eine Binärzahl umgewandelt: 100000102
9. Gleitkommazahl zusammensetzen
Als letzten Schritt werden die 3 Komponenten zu einer binären Gleitkommazahl zusammengesetzt.
Das Vorzeichenbit wurde in Schritt 3 ermittelt.
In den Exponententeil werden die in Schritt 8 berechneten Exponentenbits geschrieben. Wenn diese den Exponententeil nicht vollständig ausfüllen, wird dieser vorne mit Nullen aufgefüllt.
In den Mantissenteil gehören die Nachkommastellen der normalisierten und gerundeten Mantisse. Wenn diese den Mantissenteil nicht vollständig ausfüllen, dann wird dieser hinten mit Nullen aufgefüllt.
