Mit diesem Rechner lassen sich Dezimalzahlen zu einer binären Gleitkommazahl im IEEE-754-Format oder umgekehrt umwandeln.
Gleitkommazahlen in der IEEE-754-Darstellung haben eine feste Anzahl an Bits (meistens 32 oder 64). Mit ihnen lassen sich sowohl sehr große als auch sehr kleine Zahlen darstellen. Insbesondere Zahlen mit Nachkommastellen lassen sich aber häufig nicht exakt darstellen, weswegen oft gerundet werden muss.
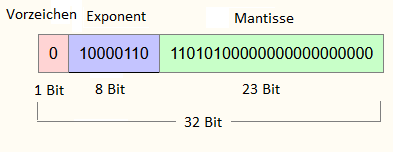
Binärzahlen in der IEEE-754-Darstellung beginnen mit einem Vorzeichen-Bit. Darauf folgen Exponenten-Bits und darauf folgt eine Mantisse. Eine binäre Gleitkommazahl mit 32 Bits hat zum Beispiel 1 Vorzeichenbit, 8 Bits für den Exponenten und 23 Bits für die Mantisse.
Formate
Es gibt mehrere Formate, in denen sich die Gleitkommazahlen darstellen lassen. Diese unterscheiden sich in der Gesamtanzahl der Bits und in der Anzahl der Bits für den Exponenten und die Mantisse. Außerdem unterscheiden sich diese in einem sogenannten Bias-Wert, welcher dazu dient auch negative Exponenten ohne zusätzliches Vorzeichen-Bit abspeichern zu können.
| Datentyp | Größe | Exponent | Mantisse | Bias |
|---|---|---|---|---|
| binary16 | 16 Bits | 5 Bits | 10 Bits | 15 |
| binary32 | 32 Bits | 8 Bits | 23 Bits | 127 |
| binary64 | 64 Bits | 11 Bits | 52 Bits | 1023 |
| binary128 | 128 Bits | 15 Bits | 112 Bits | 16383 |
Desto mehr Bits die Mantisse enthält, desto genauer lässt sich eine Zahl darstellen.
Besondere Werte
| Wert | Vorzeichen | Exponent | Mantisse |
|---|---|---|---|
| 0 | 0 oder 1 | 00000000 | 00000000000000000000000 |
| ∞ | 0 | 11111111 | 00000000000000000000000 |
| −∞ | 1 | 11111111 | 00000000000000000000000 |
| denormalisiert | 0 oder 1 | 00000000 | beliebig, aber nicht nur Nullen |
| NaN | 0 oder 1 | 11111111 | beliebig, aber nicht nur Nullen |
Dezimalzahl in Gleitkommazahl umwandeln
Eine Dezimalzahl lässt sich mit den folgenden Schritten in die IEEE-754-Gleitkommadarstellung umwandeln:
- Vorzeichenbit bestimmen
- Zahl in Binärzahl umwandeln
- Komma so verschieben, dass vor dem Komma nur noch eine 1 steht
- Runden
- zum Exponentwert Bias hinzuaddieren
- den Exponent in das Binärsystem umwandeln
- Gleitkommazahl zusammensetzen
Um das Vorgehen zu verdeutlichen soll die Zahl -42,625 als binäre Gleitkommazahl im Format binary32 dargestellt werden.
1. Vorzeichenbit bestimmen:
Wenn die Zahl positiv ist, wird in das Vorzeichenbit eine 0 geschrieben und wenn sie negativ ist eine 1.
-42,625 ist negativ. Somit kommt in das Vorzeichen-Bit eine 1.
2. Zahl in Binärzahl umwandeln:
Als nächstes muss die 42,625 in eine Binärzahl umgewandelt werden. Man erhält: 101010,1012
Dies kann man auch wie folgt schreiben: 101010,1012 ∙ 20
3. Komma so verschieben, dass vor dem Komma nur noch eine 1 steht:
Das Komma muss so verschoben werden, dass vor dem Komma genau eine 1 steht und sonst nichts mehr. Der Exponent wird entsprechend angepasst.
Das Komma wird um 5 Stellen nach links verschoben. Es gilt also: 101010,1012 ∙ 20 = 1,010101012 ∙ 25
Anmerkung: Wenn das Komma nach rechts verschoben geworden wäre, dann wäre der Exponent negativ geworden.
4. Runden:
Wenn große Zahlen oder Zahlen, die ein Komma enthalten, in eine IEEE-754-Gleitkommazahl umgewandelt werden sollen, dann kann es passieren, dass nicht alle Ziffern hinter dem Komma in die Mantisse passen. In diesem Fall muss die Zahl so gerundet werden, dass sie hinterher maximal so viele Nachkommastellen hat, wie die Mantisse Bits. Es gibt verschiedene Möglichkeiten zu Runden. Unter anderem kann immer aufgerundet, immer abgerundet oder immer gegen 0 gerundet werden. Alle 3 Methoden haben den Nachteil, dass bei langen Berechnungen, bei denen immer in die gleiche Richtung gerundet wird, sich der Rundungsfehler immer weiter vergrößert.
Es gibt noch eine vierte Variante, die normalerweise gewählt wird. Nach dieser Variante wird immer zur nächsten darstellbaren Zahl gerundet. Wenn die Zahl also näher an der nächstkleineren Zahl ist als an der nächstgrößeren, wird abgerundet (und umgekehrt). Wenn die Zahl genau in der Mitte zwischen der nächstkleineren und der nächstgrößeren Zahl liegt, dann wird zu der Zahl gerundet, die im letzten Bit der Mantisse eine 0 stehen hat. Aus statistischer Sicht wird so häufig aufgerundet, wie abgerundet und dadurch wird die Problematik mit dem sich immer weiter vergrößernden Rundungsfehler reduziert.
Wenn eine Zahl betragsmäßig zu groß ist um dargestellt zu werden (der Exponent ist vor der Einberechnung vom Bias größer als der Bias), wird auf ∞ bzw. auf −∞ gerundet.
1,010101012 hat 8 Nachkommastellen und in die Mantisse passen 23 Bits. Somit muss nicht gerundet werden.
5. zum Exponentwert Bias hinzuaddieren:
Als nächstes muss zum Wert vom Exponenten der Bias hinzuaddiert werden. Für Gleitkommazahlen mit 32 Bits beträgt der Bias 127. Also rechnet man: 5 + 127 = 132
6. den Exponent in das Binärsystem umwandeln:
Danach wird der Exponentwert, zu dem der Bias hinzuaddiert wurde, in eine Binärzahl umgewandelt.
13210 ≙ 100001002
7. Gleitkommazahl zusammensetzen:
Nun wird alles zusammengesetzt. In das Vorzeichenbit kommt der in Schritt 1 bestimmte Wert. In den Exponentteil kommt die in Schritt 6 berechnete Binärzahl. Wenn diese den Exponententeil nicht komplett ausfüllen würde, dann wird die Binärzahl um führende Nullen erweitert.
In die Mantisse werden die Bits eingetragen, die hinter dem Komma stehen. Die 1 vor dem Komma wird somit nicht mit in die Mantisse geschrieben. Wenn die Mantisse durch die Nachkommastellen nicht komplett ausgefüllt wird, werden so lange Nullen angehängt, bis die Bitzahl für die Mantisse erreicht ist. Wenn mehr Nachkommastellen vorhanden sind, als für die Mantisse Bits vorgesehen sind, muss gerundet werden.
Im Vorzeichen-Bit wird eine "1" eingetragen.
In den Exponententeil gehört die in Schritt 6 ermittelte "10000100".
In die Mantisse gehören die in Schritt 3 bestimmten Nachkommastellen "01010101". Da es nur 8 Nachkommastellen gibt, müssen noch 15 Nullen angehängt werden, um auf die benötigten 23 Bits zu kommen.
Das Ergebnis ist also:
Gleitkommazahl in Dezimalzahl umwandeln
Eine binäre Gleitkommazahl im IEEE-754-Format lässt sich mit den folgenden Schritten in eine Dezimalzahl umwandeln:
- Exponent in dezimal umrechnen
- vom Exponenten den Bias abziehen
- Mantisse um führendes "1," erweitern
- Komma verschieben
- Mantisse in Dezimalzahl umwandeln
- Vorzeichen bestimmen
Als Beispiel soll die folgende Zahl in das Dezimalsystem umgewandelt werden:
1. Exponent in dezimal umrechnen:
Als erstes wird der Exponent-Teil vom Binärsystem in das Dezimalsystem umgerechnet.
100001002 ≙ 13210
2. vom Exponenten den Bias abziehen:
Danach wird der Bias (in diesem Fall 127) vom Exponenten abgezogen.
132 - 127 = 5
3. Mantisse um führendes "1," erweitern:
Dann wird die Mantisse um "1," erweitert: 1,10111001000000000000000
4. Komma verschieben:
Als nächstes muss das Komma so weit verschoben werden, dass der Exponent 0 wird. Wenn der Exponent größer als 0 ist, muss das Komma nach rechts verschoben werden, ansonsten nach links.
1,101110012 ∙ 25 = 110111,0012 ∙ 20
5. Mantisse in Dezimalzahl umwandeln:
Das Ergebnis wird nun in das Dezimalsystem umgewandelt:
110111,0012 ≙ 55,12510
6. Vorzeichen bestimmen:
Als letztes wird sich noch das Vorzeichen-Bit angesehen. Wenn dieses 1 ist, wird vor die Zahl ein Minuszeichen geschrieben, ansonsten ist die Zahl positiv.
Das Vorzeichenbit ist 0. Also ist das Ergebnis positiv und das Ergebnis ist 55,125.
Hexadezimal-Schreibweise
Zur besseren Lesbarkeit werden Fließkommazahlen häufig nicht in Binärschreibweise sondern in Hexadezimalschreibweise angezeigt. Dafür werden jeweils 4 Bits zu einem Hexadezimalzeichen zusammengefasst.
Zum Beispiel ist 0x4208EC8B deutlich kürzer als "01000010000010001110110010001011". Das "0x" vor der Zahl bedeutet, dass es sich bei der Zahl um eine Hexadezimalzahl handelt.
Denormalisierte Zahlen
Bei der Umwandlung einer Zahl in eine Gleitkommazahl darf das Komma maximal um Bias − 1 Stellen nach rechts verschoben werden. Dies führt dazu, dass Zahlen, die sehr nah an der 0 liegen, nicht normalisiert darstellbar sind. In diesem Fall wird das Komma um genau Bias − 1 Stellen nach rechts verschoben. Dann steht vor dem Komma eine 0 statt einer 1. Danach wird die Zahl gerundet und die Nachkommastellen werden wie üblich in die Mantisse eingetragen. Im Exponent stehen nur Nullen. Mit dieser Methode lassen sich Zahlen als Gleitkommazahlen darstellen, die ansonsten nicht darstellbar wären.
Bei der Umwandlung der denormalisierten Gleitkommazahl zurück in eine Dezimalzahl, wird die Mantisse um "0," anstatt um "1," erweitert und danach wird das Komma um genau Bias − 1 nach links verschoben.